Activités mathématiques en classe de terminale technologique - 26. Méthode de Monte-Carlo
Publisher: T3 France
Editor: T3 France
Author: Boris Hanus, Isabelle Pazé, Gérald Torres
Topic: Mathematics, Computer Science
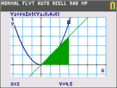
Tricks och Tips (9) - Integralberäkningar
Här tittar vi på sambandet mellan en funktion och en areafunktion. Vid undersökningarna tar vi fram arean mellan en graf och x-axeln. Vi gör detta för några funktioner av första och andra g…
Publisher: TI Sweden
Author: TI Sweden
Topic: Mathematics
Minsta arean av en förpackning | TI-84 Plus CE-T
Vilken form ska en läskburk eller konservburk ha för att minimera dess totala area och därmed mängden material till förpackningen?
Publisher: Texas Instruments Sverige | Education Technology
Author: Texas Instruments Education Technology
Topic: Mathematics
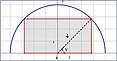
Största omkrets och area | TI-84 Plus CE-T
Kurs 4 - Teckna uttryck för en rektangels omkrets och area och bestämma det värde på x respektive v som ger den största möjliga omkretsen och arean.
Publisher: Texas Instruments Sverige | Education Technology, Texas Instruments Education Technology
Author: TI Sweden
Topic: Mathematics
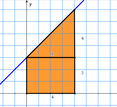
Primitiva funktioner och beräkning av areor | TI-84 Plus CE-T
Kurs 3 - För att arbeta med denna aktivitet fordras att man känner till begreppet primitiv funktion och kan beräkna sådana för enkla funktioner.
Publisher: Texas Instruments Sverige | Education Technology, TI Sweden
Topic: Mathematics
Herons formel | TI-84 Plus CE-T Python Edition
Ma 2 | Beräkna bl.a. arean av en triangel och avsluta med programmering i Python.
Publisher: Texas Instruments Sverige | Education Technology
Topic: Mathematics, STEM
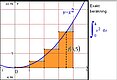
Integralberäkning med mittpunktsmetoden med programmering
Ma 4 - Derivator och integraler - Med TI-Nspire kan du göra beräkningar med integraler, både exakt och numeriskt.
Publisher: Texas Instruments Sverige | Education Technology
Author: TI Sweden
Topic: Mathematics, STEM
Functies & Grafieken
Publisher: WIL-de Wiskunde, T³ Nederland
Author: WIL-de Wiskunde
Topic: Mathematics
Functies & Grafieken
Publisher: WIL-de Wiskunde, T³ Nederland
Author: WIL-de Wiskunde
Topic: Mathematics
Graphing Calculator Software Applications (APPS) are pieces of software that can be downloaded onto a TI graphing calculator as you would add software to a computer to enhance its capabilit…
Publisher: T³ Europe
Editor: Koen Stulens
Author: Martin van Reeuwijk, Serge Etienne, Hildegard Urban-Woldron, T³ Europe
Topic: Mathematics, STEM
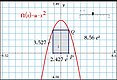
Ma 3 - Derivator och integralbegreppet - Undersöker i denna övning hur en rektangels area varierar
Author: Texas Instruments Sverige | Education Technology
Topic: Mathematics
Ma 3c - Derivator och integralbegrepp | Här viker man ett A4-papper till en triangel och undersöker hur arean ändras beroende av läget av det nedvikta hörnet.
Author: Texas Instruments Sverige | Education Technology
Topic: Mathematics
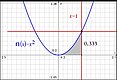
Potensfunktioner och kvoten mellan två areor
Ma 3 - Derivator och integraler | I en serie av övningar skall du studera hur kvoten av två areor inneslutna av två linjer och en potensfunktion.
Author: Texas Instruments Sverige | Education Technology
Topic: Mathematics
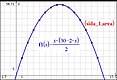
Att inhägna ett rektangulärt område
Ma 2 - Linjära och icke linjära modeller | Du vill göra inhägnaden rektangelformad.
Author: Texas Instruments Sverige | Education Technology
Topic: Mathematics
Ma 3 - Samband och förändring, Vik ett A4 papper
Author: Texas Instruments Sverige | Education Technology
Topic: Mathematics
Students consider the question "What is the shape of the curve forming the terminator of the crescent moon?" They then calculate the area of the crescent and graph its variation over one m…
Author: Ian Galloway
Topic: STEM
An activity to help students think about and appreciate simple fractions.
Publisher: Texas Instruments UK
Editor: Barrie Galpin
Author: David J C Elgin
Topic: Mathematics
Assistance to understand fractions.
Publisher: Texas Instruments UK
Editor: Barrie Galpin
Author: David J C Elgin
Topic: Mathematics