The sheep-pen problem

Recognise a quadratic in a realistic context and solve an optimisation problem
Publisher: Texas Instruments UK
Editor: Barrie Galpin
Author: Allan Duncan
Topic: Matematik
Tags Kvadratisk , Omkrets , Area , Algebra
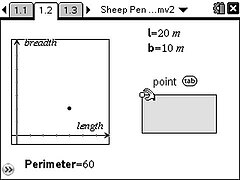
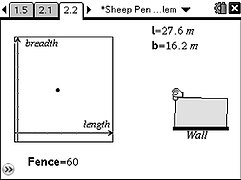
A farmer has 60m of sheep fencing and wishes to create a rectangular pen with maximum area. In the basic problem he has only the fencing to use and in the extension problem he can also use a straight wall.
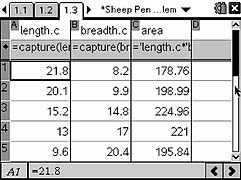
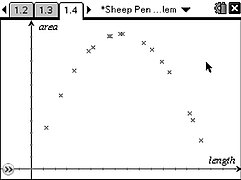
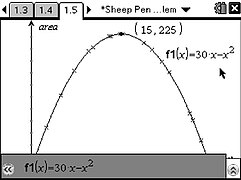
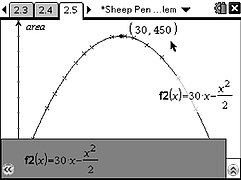
Students can experiment to see how the shape of the pen can change. By capturing dimension data to a spreadsheet, a scatterplot can be produced. The resulting parabola suggests a quadratic function and algebraic modelling confirms this.
The activity uses dynamically linked multiple representations of the maths that underlies the problem. The students use text, dynamic geometry, graphs, algebra and spreadsheets while constantly relating the maths back to the original sheep pen problem.
A lesson using this activity is described by Allan Duncan in a booklet entitled Inspired Connections in Maths Lessons. For a pdf version of the entire booklet please click here.