Materialien zum TI-30X Prio MathPrint Schulrechner
Das vorliegende Material möchte Nutzern dieses digitalen Hilfsmittels Anregungen zum Einsatz des TI-30X Prio MathPrint geben, die in den meisten Fällen über das im Handbuch Besprochene hina…
Publisher: Texas Instruments Education Technology
Author: Wilfried Zappe
Topic: Mathematics

Ein MMS wie der TI-Nspire™ CX II-T CAS bietet vielfältige Lösungsmöglichkeiten
In dem Beitrag zeigen die Autoren am Beispiel der Lösung von Bewegungsaufgaben, dass sich mit Hilfe von MMS vielfältige Lösungsmöglichkeiten nutzen lassen.
Publisher: T³ Deutschland - Materialien
Author: Hubert Langlotz, Wilfried Zappe
Topic: Mathematics
Vier-Kreise-Satz von René Descartes – weitere Beispiele
Der Beitrag behandelt den sogenannten Vier-Kreise-Satz von Descartes unter Nutzung des TI-Nspire™ CX II-T CAS.
Publisher: T³ Deutschland
Author: Hubert Langlotz, Wilfried Zappe
Topic: Mathematics
Der Weihnachtsmann verteilt Apfelsinen
Zum 1. Advent eine Aufgabe für alle, die sich für Termaufstellung und Termumformung begeistern können.
Publisher: T³ Deutschland
Author: Martin Kesting, Wilfried Zappe
Topic: Mathematics

On-Ramp to Robotics Unit 1 (Motion) with Mars Rover Challenge for TI-84 Plus CE Python
Students will learn and use foundational concepts for robotic vehicle control along with math concepts to write a program to drive their Rover around the base of the Olympus Mons volcano on…
Publisher: Texas Instruments Inc.
Topic: Computer Science, STEM
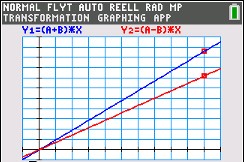
Upp och ned längs älven | TI-84 Plus CE-T
Kurs 1 - I denna aktivitet tar vi upp två lite kluriga hastighetsproblem. Här kan man arbeta både algebraiskt och grafiskt/numeriskt.
Publisher: Texas Instruments Sverige | Education Technology, TI Sweden
Topic: Mathematics
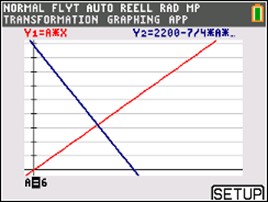
Kurs 1/Kurs 2 - I aktiviteten undersöker vi ett problem som handlar om två färjor som rör sig oavbrutet mellan två färjelägen A och B. Vi använder en av de förinstallerade apparna.
Publisher: Texas Instruments Sverige | Education Technology
Topic: Mathematics
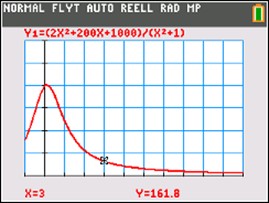
Mot oändligheten | TI-84 Plus CE-T
Kurs 3 - Vi ska i denna aktivitet gå igenom ett begrepp som kan tillämpas i många olika situationer när man sysslar med funktioner och innan man kommer in på begreppet derivata.
Publisher: Texas Instruments Sverige | Education Technology
Topic: Mathematics

Calculating the position of the James Webb Space Telescope using Python or TI-Basic
Students calculate the position of James Webb Space Telescope (JWST) using an iterative Python program in Langrange2.tns and TI-Basic in Lagrange3.tns.
Publisher: T³ Europe
Editor: Ian Galloway
Author: Veit Berger
Topic: Mathematics, Physics, Computer Science
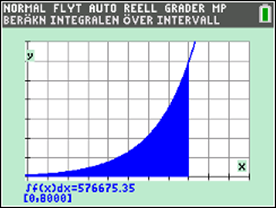
Hur många människor har någonsin levt på jorden? | TI-84 Plus CE-T
Kurs 4 - Här praktiseras både algebra, statistik och integralberäkning för att lösa ett demografiskt problem.
Publisher: Texas Instruments Sverige | Education Technology, Texas Instruments Education Technology
Topic: Mathematics

On-Ramp to Robotics Unit 1 (Motion) with Mars Rover Challenge for TI-Nspire CXII Python
Students will learn and use basic concepts for robotic vehicle control along with math concepts to write a program to drive their Rover around the base of the Olympus Mons volcano on Mars.
Publisher: Texas Instruments Inc.
Topic: Computer Science, Mathematics, STEM

TI84-Python: Sin(H)=a of Cos(H)=a oplossen
Los goniometrische vergelijkingen op.
Publisher: Jan Elemans
Editor: Jan Elemans
Author: Jan Elemans
Topic: Mathematics

TI84 Python: Kwadraat afsplitsen
Herschrijf een kwadratische vergelijking
Publisher: Jan Elemans
Editor: Jan Elemans
Author: Jan Elemans
Topic: Mathematics

DRAFT- On-Ramp to Robotics Unit 1 (Motion) Mars Rover Challenge for TI-Nspire CXII Python
Students will learn and use basic concepts for robotic vehicle control along with math concepts to write a program to drive their Rover around the base of the Olympus Mons volcano on Mars.
Publisher: Texas Instruments Inc.
Topic: Computer Science, Mathematics, STEM

TI84-Python: Wortel vereenvoudigen
Vereenvoudig de wortel.
Publisher: Jan Elemans
Editor: Jan Elemans
Author: Jan Elemans
Topic: Mathematics


Cirkel omtrek en oppervlakte TI84 Python
Omtrek en oppervlakte cirkel
Publisher: Jan Elemans
Editor: Jan Elemans
Author: Jan Elemans
Topic: Mathematics

Bepaal alle delers van een getal.
Publisher: Jan Elemans
Editor: Jan Elemans
Author: Jan Elemans
Topic: Mathematics

Exponentiele formule TI84 Python
Bepaal de exponentiele formule als je twee punten hebt.
Publisher: Jan Elemans
Editor: Jan Elemans
Author: Jan Elemans
Topic: Mathematics
